Tag Archives: talking to a computer

Science / Space Race

[May 10, 1965] A Language for the Masses (Talking to a Machine, Part Three)

2 Comments

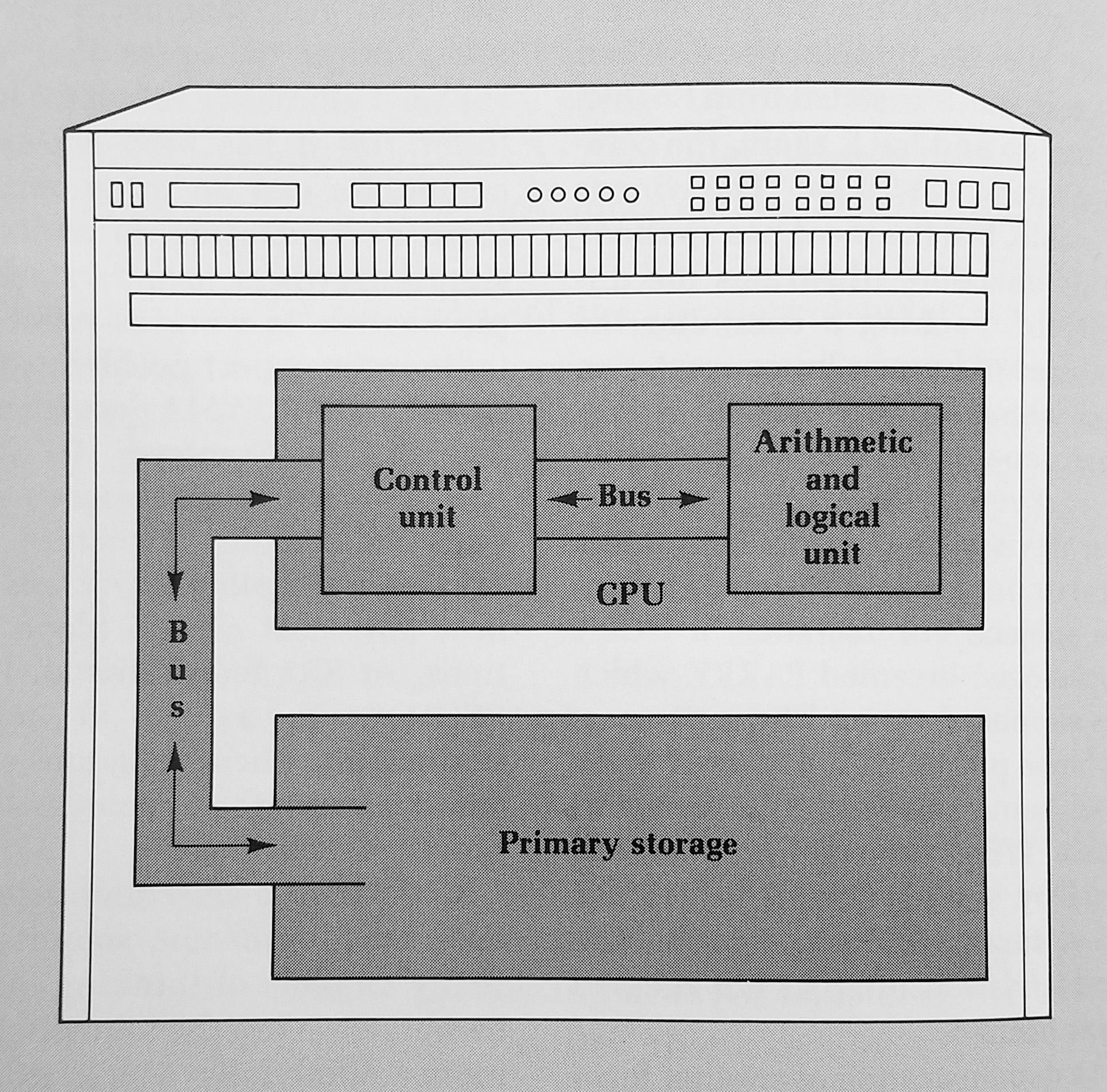
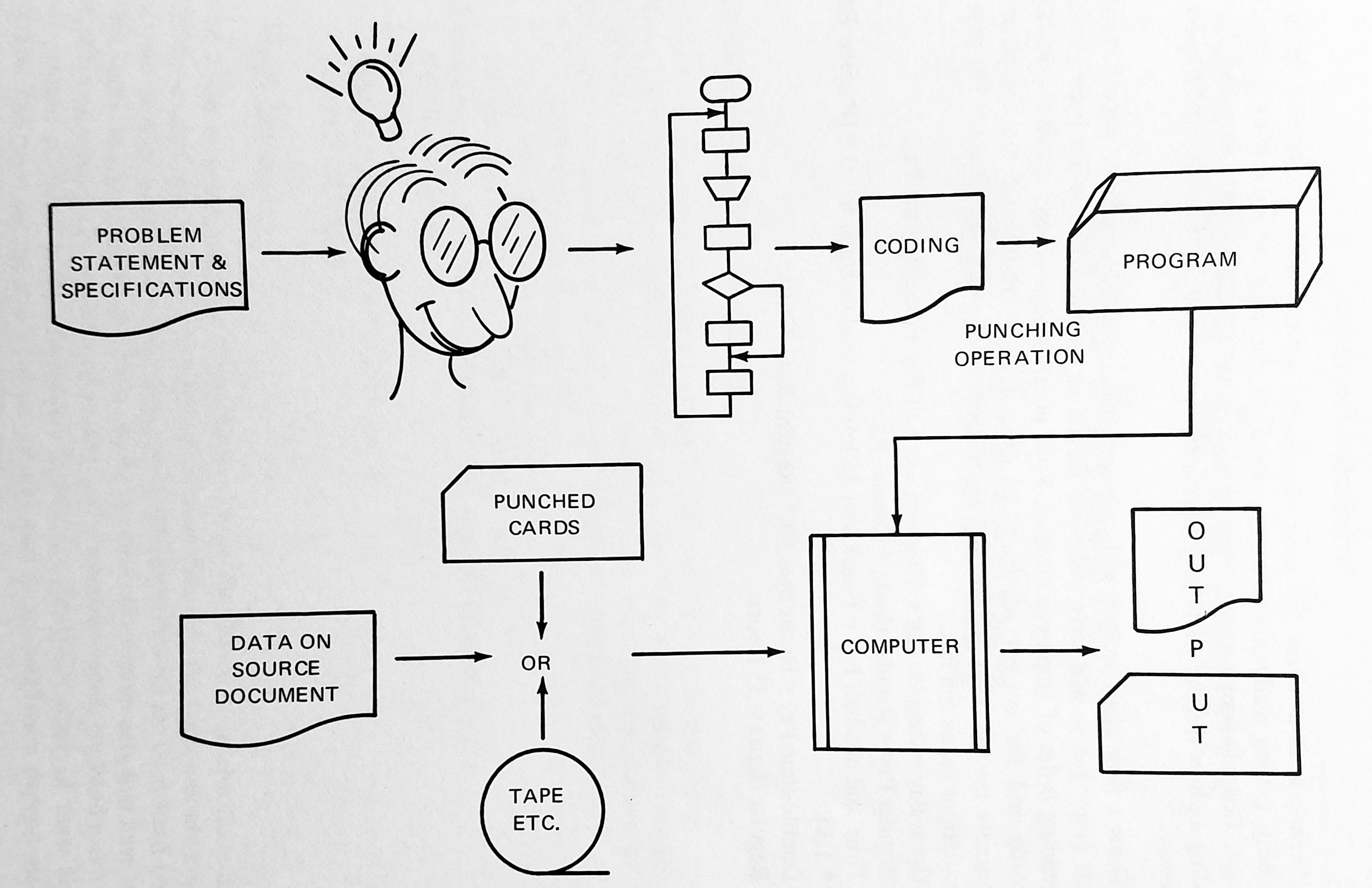
This is part three of our series on programming in the modern computer age.  Last time, we discussed the rise of user-oriented languages.  We now report on the latest of them and why it's so exciting.


by Gideon Marcus

Revolution in Mathematics

The year was 1793, and the new Republic of France was keen to carry its revolution to the standardization of weights and measures.  The Bureau du cadastre (surveying) had been tasked to construct the most accurate tables of logarithms ever produced, based on the recently developed, more convenient decimal division of the angles.  Baron Gaspard Clair François Marie Riche de Prony was given the job of computing the natural logarithm of all integers from 1 to 200,000 — to more than 14 places of accuracy!

Recognizing that there were not enough mathematicians in all of France to complete this project in a reasonable amount of time, he turned to another revolutionary concept: the assembly line.  Borrowing inspiration from the innovation as described in Adam Smith's Wealth of Nations, he divided the task into three tiers.  At the top level were the 5-6 of the most brilliant math wizards, including Adrien-Marie Legendre.  They selected the best formulas for computation of logarithms.  These formulas were then passed on to eight numerical analysts expert in calculus, who developed procedures for computation as well as error-check computations.  In today's parlance, those top mathematicians would be called "systems analysts" and the second tier folks would be "programmers."

Of course, back then, there were no digital machines to program.  Instead, de Prony assembled nearly a hundred (and perhaps more) human "computers." These men were not mathematicians; indeed, the only operations they had to conduct were addition and subtraction!  Thanks to this distributed labor system, the work was completed in just two years.

The Coming Revolution

These days, thanks to companies like IBM, Rand, and CDC, digital computers have become commonplace — more than 10,000 are currently in use!  While these machines have replaced de Prony's human calculators, they have created their own manpower shortage.  With computation so cheap and quick, and application of these computations so legion, the bottleneck is now in programmers.  What good does it do to have a hundred thousand computers in the world (a number being casually bandied about for near future years like 1972) if they sit idle with no one to feed them code?

As I showed in the first article of this series, communication between human and the first computers required rarefied skills and training.  For this reason, the first English-like programming languages were invented; they make coding more accessible and easier to learn. 

But developing programs in FORTRAN or COBOL or ALGOL is still challenging.  Each of these languages is specialized for their particular function: FORTRAN, ALGOL, and LISP are for mathematical formulas, COBOL for business and record keeping.  Moreover, all of these "higher-level" programming languages require an assembly program, a program that turns the relatively readable stuff produced by the programmer into the 1s and 0s a computer can understand.  It's an extra bit of work every time, and every code error that stalls the compiler is a wasted chunk of precious computer time.

By the early 1960s, there were folks working on both of these problems — the solution combined answers to both.

BASICally

In 1963 Dartmouth Professor John Kemeny got a grant from the National Science Foundation to implement a time-sharing system on a GE-225 computer.  Time-sharing, if you recall from Ida Moya's article last year, allows multiple users to access a computer at the same time, the machine running multiple processes simultaneously.


Photo Credit: Dartmouth College

Kemeny and his team, including Professor Thomas Kurtz and several undergrads, succeeded in completing the time-share project.  Moreover, in the interest of making computing available to everyone, they also developed a brand-new programming language. 

Beginner's All-purpose Symbolic Instruction Code, or BASIC, was the first language written specifically for novices.  In many ways, it feels similar to FORTRAN.  Here's an example of the "add two numbers" program I showed you last time:

5 PRINT "ADD TWO NUMBERS"
6 PRINT
10 READ A, B
20 LET C=A+B
30 PRINT "THE ANSWER IS", C
50 PRINT "ANOTHER? (1 FOR YES, 2 FOR NO)"
60 READ D
70 IF D = 1 THEN 6
80 IF D = 2 THEN 90
90 PRINT
100 PRINT "THANKS FOR ADDING!"
9999 END

Pretty easy to read, isn't it?

You might notice is that there's no initial declaration of variables.  You can code blithely along, and if you discover you need another variable (as I did at line 60), just go ahead and use one!  This can lead to sloppy structure, but again, the priority is ease of use without too many formal constraints. 

Indeed, there's really not much to the language — the documentation for BASIC comprises 23 pages, including sample programs.

So let me tell you the real earth-shaking thing about BASIC: the compiler is built in. 

On the Fly

Let's imagine that you are a student at Stuffy University.  Before time-sharing, if you wanted to run a program on the computer, you'd have to write the thing on paper, then punch it into cards using an off-line cardpunch, then humbly submit the cards to one of the gnomes tending the Big Machine.  He would load the FORTRAN (or whatever language) compiler into the Machine's memory.  Then he'd run your cards through the Machine's reader.  Assuming the compiler didn't choke, you might get a print-out of the program's results later that day or the next.

Now imagine that, through time-sharing, you have a terminal (a typewriter with a TV screen or printer) directly attached to the Machine.  That's a revolution in and of itself because it means you can type your code directly into a computer file.  Then you can type the commands to run the compiler program on your code, turning it into something the Machine can understand (provided the compiler doesn't choke on your bad code).

But what if, instead of that two-step process, you could enter code into a real-time compiler, one that can interpret as you code?  Then you could test individual statements, blocks of code, whole programs, without ever leaving the coding environment.  That's the revolution of BASIC.  The computer is always poised and ready to RUN the program without your having to save the code into a separate file and run a compiler on it. 


Kemeny watches his daughter, Jennifer, program — not having to bother with a compiler is particularly nice when you haven't got a screen!  Photo Credit: Dartmouth College

Moreover, you don't need to worry about arcane commands telling the program where to display output or where to find input (those numbers after every READ and WRITE command in FORTRAN.  It's all been preconfigured into the program language environment.

To be sure, making the computer keep all of these details in mind results in slower performance, but given the increased speed of machines these days and the relatively undemanding nature of BASIC programs, this is not too important. 

For the People

The goal of BASIC is to change the paradigm of computing.  If Kemeny has his way, programming will no longer be the exclusive province of the lab-coated corporate elites nor the young kooks at MIT who put together SPACEWARS!, the first computer game.  The folks at Dartmouth are trying to socialize computing, to introduce programming to people in all walks of life in anticipation of the day that there are 100,000 (or a million or a billion) computers available for use.

Vive la révolution!


Photo Credit: Dartmouth College

If you've read it this far, do me a favor and GOTO here — it's important!




2 Comments Leave A Comment
Science / Space Race

[January 2, 1965] Say that again in English? (Talking to a Machine, Part Two)

6 Comments


by Gideon Marcus

A Matter of Time

We are now in the latter half of the 1960s, and computers have become a fundamental part of our lives.  I previously discussed how computers are really quite simple, only understanding ones and zeroes.  And yet, with a bit of ingenuity and a lot of patience, a computer can be instructed ("programmed') to do almost anything.co

Patience is the operative word.  As we saw last time, when programming in a language the computer understands natively, it takes six lines of computer language ("code") to add two numbers, and thirty just to have the computer use the Pythagorean Theorem to determine the hypotenuse of a right triangle.  Can you imagine doing advanced trigonometry that way?  Simple calculus?  How about advanced calculus?

If you're a scientist, you probably know advanced mathematics, but it's unlikely that you have any idea how to write machine language code.  And given that every computer speaks its own version of machine language, you certainly couldn't be expected know how to speak to all of them in their native tongue. 

But if you've got a thorny problem to solve, and the math is too complex (or more importantly, time-consuming) for you to handle on your own, you've got to be able to use a computer.  At that point, given the tools we've got thus far, your only option would be to employ a human translator to convert your problem into something the computer can understand.

People like this don't grow on trees!  It's not as if there are freelance software programmers out there who will take a coding assignment like piecework.  Computer tenders are full-time personnel employed by the institution that bought the machine.  Their time is precious.  They can't afford to write thousands of lines of program code every time an egghead wants to run a Fourier Transformation.  Moreover, they probably aren't scientists: would a computer gnome even know linear algebra from a serial circuit?

What's needed is a machine to talk to the machine.

A Language is Born

In 1954, a ten-person team led by IBM engineer, John Backus, developed the first robot translator.  Backus wasn't interested in plane tickets or phone bills; he simply wanted it to be easier for scientists to run math equations on a computer.  Sophisticated business applications could come later.


John Backus


Lois Habit, the lone woman on the team

Backus' team created FORTRAN: Formula Translator.  And it sparked a revolution.

FORTRAN actually comprised two elements: a new programming language for humans and a robot middleman for the computer.

First, the language.  FORTRAN, like any language, has a grammar and a vocabulary.  There are dozens of words, all of them more or less recognizable to an English speaker, though their definitions are highly specific.  Also, they must be entered in a grammatically rigorous fashion for them to work. 

But once one gets the knack, its orders of magnitude easier to program in FORTRAN than machine language.  For example, last time, we saw it took six lines of code just to add two numbers, and we had to include the numbers as part of the program.  What if we wanted a general program to add any two numbers?

It'd look like this:

PROGRAM ADD

C This program will add two numbers

INTEGER FIRST, SECOND, TOTAL

10 FORMAT(I5)
20 FORMAT(I6)

READ (5,10) FIRST

READ (5,10) SECOND

TOTAL = FIRST + SECOND

WRITE (6,20) TOTAL

END

Even without explanation, you probably were able to figure out how this program works, but here's some extra information:

Every FORTRAN program starts with PROGRAM (followed by the program's name) and ends with END.  At the beginning of every program, one declares their variables, informing the computer how to label any data it manipulates.  In this case, we're playing with integers, but variables can be real numbers or even strings of text.  FORMAT tells the program how many digits the variables can have (in this case, up to five for entry, six for the total).

When a line starts with a "C", any comment (generally explanatory) may follow.  What a boon for error-checking ("debugging") that is!

If you are lucky enough to have direct keyboard access to the computer to enter ("READ") the numbers to be added, and a CRT monitor on which the computer can display ("WRITE") the results, the interaction after the program is run will take seconds.  If you have to enter information with punch cards and view the results via printer, things will take a bit longer (and the numbers in the parentheses will be different).  But that's a topic for another article.

The whole program takes just 10 lines, one of which is optional.  Sure, it's half again as long as the equivalent machine code, but it can add any two numbers rather than two pre-coded ones.

Not only that, but that thirty line Pythagorean equation program can be done in just ten lines, too!  That's because FORTRAN includes a SQRT (square root) command.  Better still, there are commands for every trigonometric function (SIN, ASIN, COS, ACOS, etc.) so with just a few more lines, you can also get information on any triangle using the Law of Sines and Law of Cosines. 

Now you can see just how powerful a programming language can be!

Robot Middleman

Every computer comes with a kind of translator already hardwired into its permanent memory.  Otherwise, it couldn't interpret (for example) 101 as "Add" and 111 as "Print".  But, as we've discussed, they are incredibly minimal.  For a computer to understand the language of FORTRAN, it has to be programmed with an extra translator called a compiler. 

The compiler is a program input into the computer in machine language, of course (how else could it understand it?), but once entered, the compiler can be run to translate any FORTRAN program.  The compiler will completely translate ("assemble") the FORTRAN commands into a machine language program and execute it. 

This process is not instantaneous, just as a conversation between two people using an interpreter requires extra time.  Moreover, the compiler-assembled program is generally not as efficiently written (i.e. it takes more lines of code) as one optimized for brevity by an expert human. 

But because one saves so much time coding in FORTRAN, and because a human machine language expert isn't needed, the result is a tremendous net increase in efficiency.  In fact, programmers have been 500% quicker in their coding as a result, and they can focus on the problem they are trying to solve rather than the daunting task of talking in ones and zeroes or some arcane machine language.  That's worth the small price in computing time inefficiency.

Programming for everyone

FORTRAN was the first "higher-level" programming language, but it was quickly joined by many others.  They include LISP ("LISt Processing"), COBOL ("COmmon Business-Oriented Language"), and ALGOL ("ALGOrithmic Language"), each with their own specialized vocabulary and capabilities.  Indeed, it would be no exaggeration to say that a computer that can't read a higher-level language is almost useless; it's no surprise that FORTRAN was developed less than a decade after ENIAC, the first computer, came on-line.

But, as amazing as all of these languages are, their usage remains daunting.  FORTRAN et. al. are very good for the applications they were designed for, but not terribly flexible for anything else.

What this means is that, while FORTRAN might be useful to a physicist for making mathematical calculations, and COBOL is great for a corporate engineer to automate inventory control, there is no language for general application.  No introductory computing language that one (say, a college student) might learn to familiarize oneself with the theory of higher-level programming.

Moreover, most people don't have direct access to a computer, which means laboriously using a keypunch machine to put holes in punchcards (with one line of code per card), giving the stack to a technician, and waiting who-knows-how-long to get a result. 

The stage has been set for a simpler, even higher-level programming language that will allow anyone to dive feet first into coding — and that's basically what we'll be talking about in the next article in this series.




6 Comments Leave A Comment
Science / Space Race

[Aug. 17, 1964] Yes and No (Talking to a Machine, Part 1)

2 Comments


by Gideon Marcus

Making sense of it all

Computers can do amazing things these days. Twenty years ago, they were vacuum tube-filled monstrosities purpose-built for calculating artillery trajectories; now, they are sleek, transistorized mini-monstrosities that do everything from calculating income tax to booking vacations across multiple airlines. It used to be that computers were mathematically inclined women — these days, digital computers do everything those able women did, and many times faster.

This is an absolute miracle when you realize just how limited a digital computer really is. It's about the dumbest, simplest thing you can imagine. Appropriately, the successful operation of a computer, and programming those operations, is one of the more abstruse topics I've come across. Certainly, no one has ever been able to give me a concise education on the subject.

I'm a naive (or arrogant) person. I'm going to try to give you one. It's a complex topic, though, so I'm going to try to break it into "bite"-sized parts. Read on for part one!

Ones and Zeroes

Whether you know it or not, you are already familiar with the concept of binary. Your light switch is either on or off. Your television, your radio, your blender — all of them are either in operation or not. There is no in-between (or, at least, there shouldn't be).

A digital computer is nothing but a big bunch of places where you process ons and offs; for simplicity's sake, let's call an off "0" and an on "1". Inside every computer is a place for storing 1s and 0s called its "memory". If you've ever seen medieval chain mail, you have an idea what it looks like, a net of metal rings, each of which can be individually magnetized. If a ring is magnetized, the computer sees it as on or "1". If not, it sees it as off or "0".

Now, there's not a lot of information you can store there — just the on/off state. But what if you grouped of eight of these binary digits (or "bits") so that your computer knew they were associated? Then you could have all sorts of 8-digit groups (called "bytes"). For instance:

00000000
11111111
11110000
00001111
10000001

and so on. All told, you could have 256 combinations of ones and zeroes in each of these groups, and that's enough to be useful. Here's how.

Three simple tasks

A computer, at its heart, can do just three things:

  1. Store information. Think of a computer's memory as a post office, and each byte is a mailbox. In fact, in computing, these mailboxes are called addresses. Each address can store one of the 256 combinations of ones and zeroes.
  2. Do arithmetic. A computer is designed to be able to add, subtract, multiply, and divide.
  3. Compare numbers. A computer can look at two different numbers and tell you if one is equal to, greater than, or less than the other.

That's it! When I first learned that, I (like you) wondered "how the heck can something like that do something complicated like making sure my Allegheny Airlines reservation gets transferred to Eastern for my trip to New York?"

As it turns out, these three basic computer functions are sufficient for that task — if you are clever in how you instruct a computer to do them.

Talking in numbers

Remember that a computer can only speak in binary digits ("binary" for short.) Let's say a computer has been hard-coded to know that when you input "110", you mean "store the following number in the following address." If you input "101" it means "add the number in the following address to whatever is in this other, following address. And let's say "111" means "print out whatever is in the following address."

A very simple program, computing A + B = C might look like this (for the sake of simplicity, let's say that your computer's memory has 256 addresses in which it can store bytes, each addressed with digits 00000001 through 11111111):

  1. 110 1 00000001
  2. 110 10 00000010
  3. 110 0 000000011
  4. 101 000000001 00000011
  5. 101 000000010 00000011
  6. 111 000000011

In English, that's:

  1. Put "1" in address #1.
  2. Put "2" in address #2.

    3. (how does 10 equal 2? Just like when you add 1 to 9 in normal, base 10 arithmetic, you make the ones place 0 and carry the one into the tens place.  In binary, 1 is the most that can ever fit into a digit — so if you add 1, you make that place zero and carry the 1 to the next place over.

    Thus 1 + 1 = 10 (2), 10 (2) + 1 = 11 (3), 10 (2) + 10 (2) = 100 (4) …and 11111111 =255!)

  3. Put "0" in address #3 (just to make sure we're starting from zero — if a program had used that byte before, it might not be empty!)
  4. Add whatever is in address #1 (in this case, 1) to whatever's in address #3 (so far, nothing).
  5. Add whatever is in address #2 (in this case, 2) to whatever's in address #3 (so far, 1).
  6. Show me what's in address #3: The answer should be "3" (because 1+2=3). Except, it will probably be displayed as "11" because this is a computer we're talking about.

Good grief, that's a headache, and that's just for one simple bit of math. The first big problem is just remembering the commands. How is anyone supposed to look at that code and know what those initial numbers mean?

An easier way

The folks at IBM, Univac, CDC, etc. solved that particular problem pretty easily. They designed a program (entered in binary) that translates easier-to-remember three letter alphanumeric codes into binary numbers. Thus, someone could write the above program as, for example:

  1. STO 1 00000001
  2. STO 10 00000010
  3. STO 11 00000000
  4. ADD 000000001 00000011
  5. ADD 000000010 00000011
  6. SHO 000000011

STO, ADD, and SHO make a bit more intuitive sense than strings of numbers, after all.

And since you can translate letters to binary, why not numbers and addresses?

  1. STO 1 A1
  2. STO 2 A2
  3. STO 0 A3
  4. ADD A1 A3
  5. ADD A2 A3
  6. SHO A3

Note, these are not commands in any actual language — I made them up. And each computer system will have its own set of commands unique to the system, but real code will look something like this.

This easier to understand, mnemonic language is called "Assembly" because the program assembles your commands into something the computer understands (remember — they only know ones and zeroes).

Hitting the ceiling

Assembly makes it easier to program a computer, but it's still tedious. Just adding 1+2 took five lines. Imagine wanting to do something simple like computing the hypotenuse of a right triangle:

In geometry class, we learned that A2 + B2 = C2.

The first part of that is easy enough.

  1. STO A A1 (store A in address A1)
  2. STO B A2 (store B in address A2)
  3. STO 0 A3 (Clear out address A3 for use)
  4. MUL A1 A1 (multiply what's in A1 by itself)
  5. MUL A2 A2 (multiple what's in A2 by itself)
  6. ADD A1 A3 (add what's now in A1 to what's in A3)
  7. ADD A2 A3 (add what's now in A2 to what's in A3)

All right. That gets us A2 + B2 in the third address…but how do we get the square root of C2?

When I wrote this, I had no idea. I've since talked to a programmer. She showed me a thirty line program that I still don't understand. Sure, it works, but thirty lines for a simple equation? There has to be an easier way, one that doesn't involve me pulling out my accursed slide rule.

There is! To find out how, join us for the next installment of this series!

[Come join us at Portal 55, Galactic Journey's real-time lounge! Talk about your favorite SFF, chat with the Traveler and co., relax, sit a spell…]




2 Comments Leave A Comment